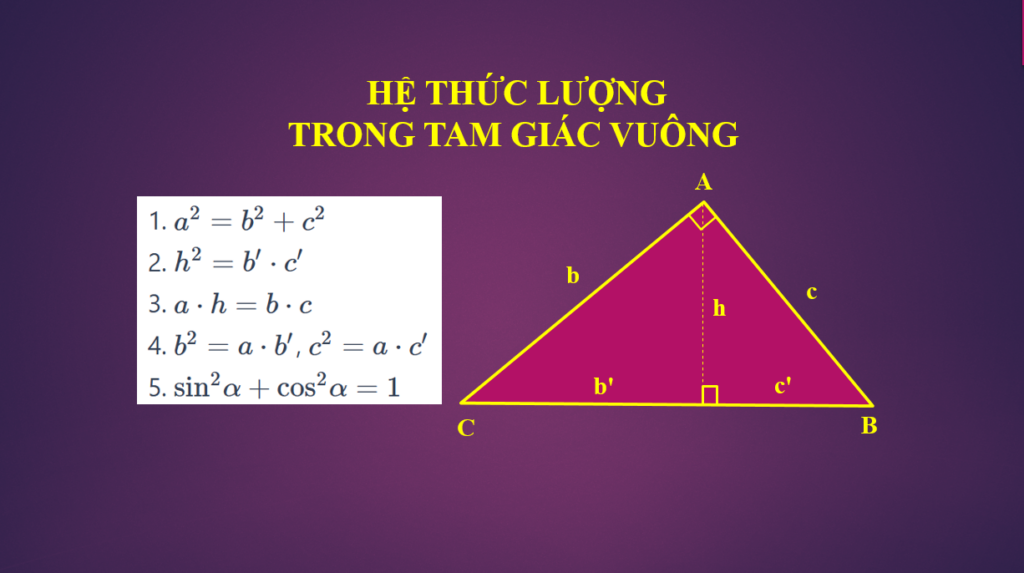
Hệ Thức Lượng Trong Tam Giác Vuông

Hệ thức lượng trong tam giác vuông là một trong những viên gạch nền tảng của toán học, một kiến thức không thể thiếu mà mỗi học sinh lớp 9 cần phải nắm vững. Những công thức này không chỉ là chìa khóa để giải nhanh các bài toán hình học, mà còn là cầu nối giúp bạn khám phá vẻ đẹp logic và kỳ diệu của toán học. Để học tập hiệu quả và đạt kết quả tốt nhất, việc thấu hiểu và ghi nhớ các hệ thức này là điều vô cùng quan trọng. Hãy cùng hethucluong.com khám phá những Hệ thức lượng trong tam giác vuông được tổng hợp dưới đây, để hành trình chinh phục toán học của bạn trở nên dễ dàng và thú vị hơn bao giờ hết!

1. Tam Giác Vuông Và Các Yếu Tố Cơ Bản

1.1. Định nghĩa tam giác vuông

Tam giác vuông là tam giác có một góc bằng $90°$ (góc vuông). Cạnh đối diện với góc vuông được gọi là cạnh huyền, hai cạnh còn lại gọi là cạnh góc vuông.

1.2. Quy ước ký hiệu

Cho tam giác $ABC$ vuông tại $A$, có đường cao $AH$ với $H \in BC$.

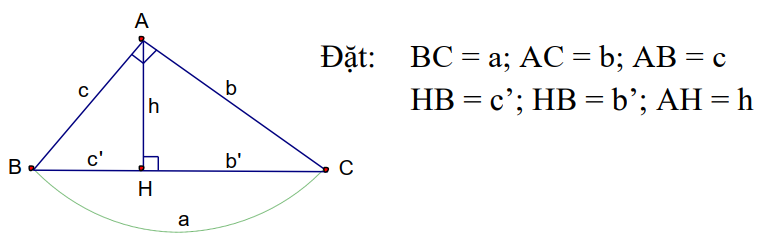
Ký hiệu các cạnh:

• $BC = a$ (cạnh huyền)
• $AC = b$ (cạnh góc vuông)
• $AB = c$ (cạnh góc vuông)

Ký hiệu đường cao và hình chiếu:

• $AH = h$ (đường cao ứng với cạnh huyền)
• $BH = c’$ (hình chiếu của $AB$ lên $BC$)
• $CH = b’$ (hình chiếu của $AC$ lên $BC$)

Các góc:

• $\angle BAC = 90°$
• $\angle ABC = B$
• $\angle ACB = C$

1.3. Tính chất cơ bản

• Cạnh huyền là cạnh lớn nhất trong tam giác vuông
• Hai góc nhọn phụ nhau: $B + C = 90°$
• Tổng hai hình chiếu bằng cạnh huyền: $b’ + c’ = a$

2. Định Lý Pythagore

2.1. Phát biểu định lý

Định lý Pythagore: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

$a^2 = b^2 + c^2$

Hoặc:

$BC^2 = AB^2 + AC^2$

2.2. Định lý đảo

Nếu một tam giác có bình phương một cạnh bằng tổng bình phương hai cạnh kia, thì tam giác đó là tam giác vuông.

Nếu $a^2 = b^2 + c^2$ thì tam giác $ABC$ vuông tại $A$.

2.3. Các công thức suy ra

Từ định lý Pythagore, ta có thể tính:

$a = \sqrt{b^2 + c^2}$

$b = \sqrt{a^2 – c^2}$

$c = \sqrt{a^2 – b^2}$

2.4. Bộ ba Pythagore phổ biến

Các bộ ba số nguyên dương $(a, b, c)$ thỏa mãn $a^2 = b^2 + c^2$:

• $(3, 4, 5)$ và các bội số: $(6, 8, 10)$, $(9, 12, 15)$, $(12, 16, 20)$…
• $(5, 12, 13)$ và các bội số: $(10, 24, 26)$…
• $(8, 15, 17)$
• $(7, 24, 25)$
• $(20, 21, 29)$

Mẹo: Khi gặp các số này trong đề bài, bạn có thể nhận biết ngay đây là tam giác vuông mà không cần tính toán.

2.5. Ví dụ minh họa

Ví dụ 1: Tam giác có ba cạnh lần lượt là 9 cm, 12 cm, 15 cm. Tam giác này có vuông không?

Lời giải

Kiểm tra: $15^2 = 225$ và $9^2 + 12^2 = 81 + 144 = 225$

Vì $15^2 = 9^2 + 12^2$ nên tam giác này vuông (tại đỉnh đối diện với cạnh 15 cm).

Ví dụ 2: Cho tam giác vuông có cạnh huyền 10 cm, một cạnh góc vuông 6 cm. Tính cạnh góc vuông còn lại.

Lời giải

Áp dụng định lý Pythagore:

$c = \sqrt{a^2 – b^2} = \sqrt{10^2 – 6^2} = \sqrt{100 – 36} = \sqrt{64} = 8 \text{ cm}$

3. Hệ Thức Về Đường Cao

3.1. Công thức cơ bản

Trong tam giác vuông có đường cao ứng với cạnh huyền, ta có hai hệ thức quan trọng:

Hệ thức 1: Bình phương đường cao bằng tích hai hình chiếu của các cạnh góc vuông lên cạnh huyền.

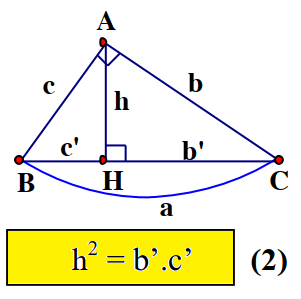
$h^2 = b’ \cdot c’$

Hoặc:

$AH^2 = BH \cdot CH$

Hệ thức 2: Tích của cạnh huyền và đường cao bằng tích hai cạnh góc vuông.

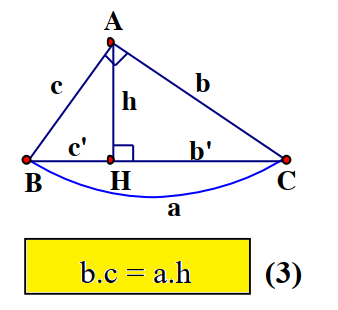
$a \cdot h = b \cdot c$

Hoặc:

$BC \cdot AH = AB \cdot AC$

3.2. Chứng minh

Chứng minh hệ thức 1:

Khi kẻ đường cao $AH$, tam giác $ABC$ được chia thành hai tam giác vuông nhỏ: $ABH$ và $ACH$.

Xét $\triangle ABH$ và $\triangle CHA$:

• Có $\angle AHB = \angle AHC = 90°$
• Có $\angle B$ chung với $\angle HAC$ (cùng phụ với $\angle BAH$)

Do đó $\triangle ABH \sim \triangle CHA$ (g.g)

Từ tỉ lệ đồng dạng: $\frac{AH}{CH} = \frac{BH}{AH}$

Suy ra: $AH^2 = BH \cdot CH$ hay $h^2 = b’ \cdot c’$

Chứng minh hệ thức 2:

Diện tích tam giác $ABC$ có thể tính theo hai cách:

Cách 1: Lấy hai cạnh góc vuông làm đáy và chiều cao: $S = \frac{1}{2} \cdot AB \cdot AC = \frac{1}{2}bc$

Cách 2: Lấy cạnh huyền làm đáy, đường cao $AH$ làm chiều cao: $S = \frac{1}{2} \cdot BC \cdot AH = \frac{1}{2}ah$

Từ đó: $\frac{1}{2}bc = \frac{1}{2}ah$

Suy ra: $a \cdot h = b \cdot c$

3.3. Các công thức suy ra

Từ hai hệ thức trên, ta có thể tính:

$h = \sqrt{b’ \cdot c’}$

$h = \frac{b \cdot c}{a}$

$b = \frac{a \cdot h}{c}$

$c = \frac{a \cdot h}{b}$

3.4. Bài tập vận dụng

Bài tập 1: Tam giác vuông có cạnh huyền 13 cm. Đường cao chia cạnh huyền thành hai đoạn có độ dài 4 cm và 9 cm. Tính độ dài đường cao.

Lời giải

Áp dụng $h^2 = b’ \cdot c’$:

$h^2 = 4 \times 9 = 36$

$h = 6 \text{ cm}$

Bài tập 2: Tam giác vuông có hai cạnh góc vuông là 5 cm và 12 cm. Tính đường cao ứng với cạnh huyền.

Lời giải

Bước 1: Tính cạnh huyền $a = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \text{ cm}$

Bước 2: Tính đường cao $h = \frac{b \cdot c}{a} = \frac{5 \times 12}{13} = \frac{60}{13} \approx 4{,}62 \text{ cm}$

4. Hệ Thức Về Hình Chiếu

4.1. Công thức chính

Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền với hình chiếu của cạnh đó lên cạnh huyền.

$b^2 = a \cdot b’$

$c^2 = a \cdot c’$

Hoặc viết đầy đủ:

$AC^2 = BC \cdot CH$

$AB^2 = BC \cdot BH$

4.2. Chứng minh

Chứng minh công thức $b^2 = a \cdot b’$:

Xét $\triangle ABC$ và $\triangle HCA$:

• Có $\angle C$ chung
• Có $\angle BAC = \angle AHC = 90°$

Do đó $\triangle ABC \sim \triangle HCA$ (g.g)

Từ tỉ lệ đồng dạng: $\frac{AC}{HC} = \frac{BC}{AC}$

Suy ra: $AC^2 = BC \cdot HC$ hay $b^2 = a \cdot b’$

Chứng minh tương tự cho $c^2 = a \cdot c’$.

4.3. Các công thức suy ra

$b = \sqrt{a \cdot b’}$

$c = \sqrt{a \cdot c’}$

$b’ = \frac{b^2}{a}$

$c’ = \frac{c^2}{a}$

4.4. Mối liên hệ giữa các hệ thức

Cộng hai công thức:

$b^2 + c^2 = a \cdot b’ + a \cdot c’ = a(b’ + c’) = a \cdot a = a^2$

Ta thu lại được định lý Pythagore!

4.5. Bài tập thực hành

Bài tập 3: Tam giác vuông có cạnh huyền 20 cm, một cạnh góc vuông 12 cm. Tính hình chiếu của cạnh đó lên cạnh huyền.

Lời giải

Áp dụng $b^2 = a \cdot b’$:

$12^2 = 20 \times b’$

$144 = 20b’$

$b’ = \frac{144}{20} = 7{,}2 \text{ cm}$

Bài tập 4: Hình chiếu của hai cạnh góc vuông lên cạnh huyền lần lượt là 3 cm và 12 cm. Tính độ dài các cạnh của tam giác.

Lời giải

Cạnh huyền: $a = b’ + c’ = 3 + 12 = 15 \text{ cm}$

Cạnh góc vuông thứ nhất: $b = \sqrt{a \cdot b’} = \sqrt{15 \times 3} = \sqrt{45} = 3\sqrt{5} \text{ cm}$

Cạnh góc vuông thứ hai: $c = \sqrt{a \cdot c’} = \sqrt{15 \times 12} = \sqrt{180} = 6\sqrt{5} \text{ cm}$

5. Hệ Thức Nghịch Đảo

5.1. Công thức

Nghịch đảo bình phương đường cao bằng tổng nghịch đảo bình phương hai cạnh góc vuông:

$\frac{1}{h^2} = \frac{1}{b^2} + \frac{1}{c^2}$

5.2. Chứng minh

Từ $a \cdot h = b \cdot c$, suy ra:

$h = \frac{bc}{a}$

Bình phương hai vế:

$h^2 = \frac{b^2c^2}{a^2}$

Nghịch đảo:

$\frac{1}{h^2} = \frac{a^2}{b^2c^2}$

Áp dụng Pythagore $a^2 = b^2 + c^2$:

$\frac{1}{h^2} = \frac{b^2 + c^2}{b^2c^2} = \frac{b^2}{b^2c^2} + \frac{c^2}{b^2c^2} = \frac{1}{c^2} + \frac{1}{b^2}$

5.3. Công thức biến đổi khác

Từ công thức trên, ta có thể viết:

$h = \frac{1}{\sqrt{\frac{1}{b^2} + \frac{1}{c^2}}}$

Hoặc:

$h = \frac{bc}{\sqrt{b^2 + c^2}}$

5.4. Ví dụ áp dụng

Ví dụ 3: Tam giác vuông có hai cạnh góc vuông là 6 cm và 8 cm. Tính đường cao ứng với cạnh huyền bằng công thức nghịch đảo.

Lời giải:

$\frac{1}{h^2} = \frac{1}{6^2} + \frac{1}{8^2} = \frac{1}{36} + \frac{1}{64}$

$\frac{1}{h^2} = \frac{64 + 36}{36 \times 64} = \frac{100}{2304}$

$h^2 = \frac{2304}{100} = 23{,}04$

$h = 4{,}8 \text{ cm}$

Kiểm tra bằng công thức khác: $h = \frac{6 \times 8}{10} = 4{,}8 \text{ cm}$ ✓

6. Tỉ Số Lượng Giác Trong Tam Giác Vuông

6.1. Định nghĩa các tỉ số

Trong tam giác vuông $ABC$ vuông tại $A$, với góc nhọn $B$:

Sin (sine – sin): $\sin B = \frac{\text{cạnh đối}}{\text{cạnh huyền}} = \frac{AC}{BC} = \frac{b}{a}$

Cos (cosine – cosin): $\cos B = \frac{\text{cạnh kề}}{\text{cạnh huyền}} = \frac{AB}{BC} = \frac{c}{a}$

Tang (tangent – tang): $\tan B = \frac{\text{cạnh đối}}{\text{cạnh kề}} = \frac{AC}{AB} = \frac{b}{c}$

Cotang (cotangent – cotang): $\cot B = \frac{\text{cạnh kề}}{\text{cạnh đối}} = \frac{AB}{AC} = \frac{c}{b}$

Cách nhớ: “Sin Đối, Cos Kề, Tan Đối Kề“

6.2. Các hệ thức lượng giác cơ bản

Hệ thức Pythagore lượng giác: $\sin^2 B + \cos^2 B = 1$

Quan hệ giữa tan và cot: $\tan B \cdot \cot B = 1$

$\tan B = \frac{1}{\cot B}$

$\cot B = \frac{1}{\tan B}$

Quan hệ giữa sin, cos và tan: $\tan B = \frac{\sin B}{\cos B}$

$\cot B = \frac{\cos B}{\sin B}$

Các hệ thức khác: $1 + \tan^2 B = \frac{1}{\cos^2 B}$

$1 + \cot^2 B = \frac{1}{\sin^2 B}$

6.3. Tỉ số lượng giác của hai góc phụ nhau

Vì $B + C = 90°$, ta có:

$\sin B = \cos C = \cos(90° – B)$

$\cos B = \sin C = \sin(90° – B)$

$\tan B = \cot C = \cot(90° – B)$

$\cot B = \tan C = \tan(90° – B)$

6.4. Bảng giá trị lượng giác đặc biệt

Góc	$0°$	$30°$	$45°$	$60°$	$90°$
sin	$0$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	$1$
cos	$1$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	$0$
tan	$0$	$\frac{\sqrt{3}}{3}$	$1$	$\sqrt{3}$	Không xác định
cot	Không xác định	$\sqrt{3}$	$1$	$\frac{\sqrt{3}}{3}$	$0$

Mẹo nhớ nhanh:

Sin và cos của $30°$, $45°$, $60°$:

• Viết các số $1, 2, 3, 4$ theo hàng ngang
• Chia cho 2: $\frac{1}{2}, \frac{2}{2}, \frac{3}{2}, \frac{4}{2}$
• Lấy căn tử số: $\frac{\sqrt{1}}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}, \frac{\sqrt{4}}{2}$
• Rút gọn: $\frac{1}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}, 1$
• Đây chính là sin của $30°, 45°, 60°, 90°$
• Cos thì ngược lại (giảm dần)

6.5. Ví dụ minh họa

Ví dụ 1: Cho tam giác vuông $ABC$ vuông tại $A$, biết $\angle B = 30°$ và $BC = 10$ cm. Tính $AB$ và $AC$.

Lời giải

$\sin B = \frac{AC}{BC}$ nên $AC = BC \cdot \sin 30° = 10 \times \frac{1}{2} = 5 \text{ cm}$

$\cos B = \frac{AB}{BC}$ nên $AB = BC \cdot \cos 30° = 10 \times \frac{\sqrt{3}}{2} = 5\sqrt{3} \text{ cm}$

Ví dụ 2: Tam giác vuông cân có cạnh huyền 10 cm. Tính các cạnh góc vuông.

Lời giải

Tam giác vuông cân có hai góc nhọn đều bằng $45°$.

$b = c = a \cdot \sin 45° = 10 \times \frac{\sqrt{2}}{2} = 5\sqrt{2} \text{ cm}$

7. Bảng Tổng Hợp Công Thức

7.1. Định lý Pythagore

$a^2 = b^2 + c^2$

$a = \sqrt{b^2 + c^2}$

$b = \sqrt{a^2 – c^2}$

$c = \sqrt{a^2 – b^2}$

7.2. Hệ thức về đường cao

$h^2 = b’ \cdot c’$

$a \cdot h = b \cdot c$

$h = \sqrt{b’ \cdot c’}$

$h = \frac{b \cdot c}{a}$

7.3. Hệ thức về hình chiếu

$b^2 = a \cdot b’$

$c^2 = a \cdot c’$

$b = \sqrt{a \cdot b’}$

$c = \sqrt{a \cdot c’}$

$b’ = \frac{b^2}{a}$

$c’ = \frac{c^2}{a}$

7.4. Hệ thức nghịch đảo

$\frac{1}{h^2} = \frac{1}{b^2} + \frac{1}{c^2}$

7.5. Tỉ số lượng giác

$\sin B = \frac{b}{a}$

$\cos B = \frac{c}{a}$

$\tan B = \frac{b}{c}$

$\cot B = \frac{c}{b}$

$\sin^2 B + \cos^2 B = 1$

$\tan B \cdot \cot B = 1$

$\tan B = \frac{\sin B}{\cos B}$

7.6. Công thức kết hợp

$b’ + c’ = a$

$B + C = 90°$

$\sin B = \cos C$

$\tan B = \cot C$

8. Phương Pháp Giải Các Dạng Bài Tập

Dạng 1: Tính độ dài cạnh

Phương pháp:

1. Vẽ hình, ghi giả thiết, kết luận
2. Xác định các yếu tố đã biết
3. Chọn công thức phù hợp (ưu tiên Pythagore nếu biết hai cạnh)
4. Tính toán và đơn giản hóa kết quả
5. Kiểm tra tính hợp lý (cạnh huyền phải lớn nhất)

Ví dụ: Tam giác vuông có cạnh huyền 25 cm, một cạnh góc vuông 7 cm. Tính cạnh góc vuông còn lại.

Giải

$c = \sqrt{a^2 – b^2} = \sqrt{25^2 – 7^2} = \sqrt{625 – 49} = \sqrt{576} = 24 \text{ cm}$

Dạng 2: Tính đường cao và hình chiếu

Phương pháp:

1. Nếu biết hai cạnh góc vuông: Tính cạnh huyền trước, sau đó dùng $a \cdot h = b \cdot c$
2. Nếu biết hình chiếu: Dùng $h^2 = b’ \cdot c’$
3. Nếu biết cạnh và hình chiếu của nó: Dùng $b^2 = a \cdot b’$ hoặc $c^2 = a \cdot c’$

Ví dụ: Tam giác vuông có hai cạnh góc vuông 9 cm và 12 cm. Tính đường cao, cạnh huyền và các hình chiếu.

Giải

Cạnh huyền: $a = \sqrt{9^2 + 12^2} = 15 \text{ cm}$

Đường cao: $h = \frac{9 \times 12}{15} = \frac{108}{15} = 7{,}2 \text{ cm}$

Hình chiếu của cạnh 9 cm: $b’ = \frac{9^2}{15} = \frac{81}{15} = 5{,}4 \text{ cm}$

Hình chiếu của cạnh 12 cm: $c’ = \frac{12^2}{15} = \frac{144}{15} = 9{,}6 \text{ cm}$

Kiểm tra: $5{,}4 + 9{,}6 = 15$ ✓

Dạng 3: Chứng minh hệ thức

Phương pháp:

1. Sử dụng các hệ thức đã biết
2. Biến đổi đại số (nhân, chia, cộng, trừ hai vế)
3. Sử dụng định lý về tam giác đồng dạng
4. Thay thế và rút gọn

Ví dụ: Chứng minh $\frac{1}{b^2} + \frac{1}{c^2} = \frac{1}{h^2}$

Giải

Ta có: $a \cdot h = b \cdot c$ nên $h = \frac{bc}{a}$

$\frac{1}{h^2} = \frac{a^2}{b^2c^2}$

Mà $a^2 = b^2 + c^2$ (Pythagore)

$\frac{1}{h^2} = \frac{b^2 + c^2}{b^2c^2} = \frac{b^2}{b^2c^2} + \frac{c^2}{b^2c^2} = \frac{1}{c^2} + \frac{1}{b^2}$

Dạng 4: Bài toán thực tế

Phương pháp:

1. Đọc kỹ đề, hiểu bài toán
2. Vẽ hình minh họa, chuyển về bài toán hình học
3. Xác định tam giác vuông trong tình huống thực tế
4. Áp dụng các hệ thức hoặc tỉ số lượng giác
5. Tính toán và đưa ra kết quả có ý nghĩa thực tế

Ví dụ: Một cái thang dài 5 m đặt tựa vào tường. Chân thang cách chân tường 3 m. Hỏi đầu thang cách mặt đất bao nhiêu mét?

Giải

Gọi chiều cao đầu thang so với mặt đất là $h$.

Áp dụng Pythagore: $h = \sqrt{5^2 – 3^2} = \sqrt{25 – 9} = \sqrt{16} = 4 \text{ m}$

Vậy đầu thang cách mặt đất 4 m.

Dạng 5: Tính góc – Sử dụng tỉ số lượng giác

Phương pháp:

1. Xác định các cạnh liên quan đến góc cần tìm
2. Chọn tỉ số lượng giác phù hợp (sin, cos, tan, cot)
3. Tính giá trị tỉ số
4. Tra bảng hoặc sử dụng máy tính để tìm góc
5. Hoặc so sánh với các giá trị đặc biệt ($30°, 45°, 60°$)

Ví dụ: Tam giác vuông có hai cạnh góc vuông bằng nhau và cạnh huyền 10 cm. Tính các góc của tam giác.

Giải

Vì hai cạnh góc vuông bằng nhau nên đây là tam giác vuông cân.

Hai góc nhọn bằng nhau và tổng bằng $90°$.

Vậy mỗi góc nhọn bằng $45°$.

Hoặc tính bằng tỉ số: $\tan B = \frac{b}{c} = 1$ nên $B = 45°$

Dạng 6: Bài toán tổng hợp

Phương pháp:

1. Phân tích đề bài, chia nhỏ bài toán
2. Giải quyết từng bước một
3. Kết hợp nhiều hệ thức
4. Kiểm tra kết quả sau mỗi bước

Ví dụ: Tam giác vuông có tỉ số hai cạnh góc vuông là $3:4$ và chu vi bằng 36 cm. Tính diện tích tam giác.

Giải

Gọi hai cạnh góc vuông là $3k$ và $4k$ ($k > 0$).

Cạnh huyền: $a = \sqrt{(3k)^2 + (4k)^2} = \sqrt{9k^2 + 16k^2} = 5k$

Chu vi: $3k + 4k + 5k = 36$

$12k = 36$

$k = 3$

Vậy hai cạnh góc vuông là $9$ cm và $12$ cm.

Diện tích: $S = \frac{1}{2} \times 9 \times 12 = 54 \text{ cm}^2$

9. Bài Tập

9.1 Bài tập có lời giải

Ví dụ 1: Tìm x và y trong hình vẽ

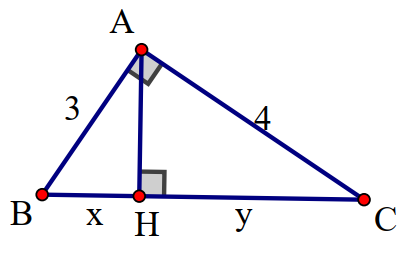
Ví dụ 2: Tìm x trong hình vẽ

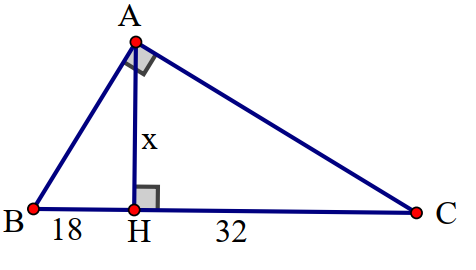
Lời giải

Ví dụ 3: Tìm x trong hình vẽ

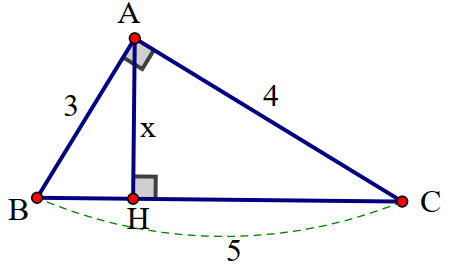
Lời giải

Ví dụ 4: Tìm x trong hình vẽ

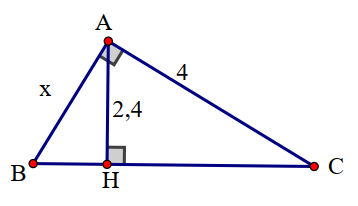
Lời giải

Bài 5: Tam giác $ABC$ vuông tại $A$, có $AB = 6$ cm, $AC = 8$ cm. Kẻ đường cao $AH$. a) Tính $BC$ b) Tính $AH$ c) Tính $BH$ và $CH$

Lời giải

a) Áp dụng Pythagore: $BC = \sqrt{AB^2 + AC^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = 10 \text{ cm}$

b) Áp dụng công thức: $AH = \frac{AB \cdot AC}{BC} = \frac{6 \times 8}{10} = 4{,}8 \text{ cm}$

c) Áp dụng công thức hình chiếu: $BH = \frac{AB^2}{BC} = \frac{36}{10} = 3{,}6 \text{ cm}$

$CH = \frac{AC^2}{BC} = \frac{64}{10} = 6{,}4 \text{ cm}$

Kiểm tra: $BH + CH = 3{,}6 + 6{,}4 = 10$ cm ✓

Bài 6: Cho tam giác vuông có cạnh huyền 15 cm và một góc nhọn $60°$. Tính các cạnh góc vuông.

Lời giải

Gọi góc $B = 60°$, cạnh huyền $BC = 15$ cm.

Cạnh đối diện góc $60°$: $AC = BC \cdot \sin 60° = 15 \times \frac{\sqrt{3}}{2} = \frac{15\sqrt{3}}{2} \approx 12{,}99 \text{ cm}$

Cạnh kề góc $60°$: $AB = BC \cdot \cos 60° = 15 \times \frac{1}{2} = 7{,}5 \text{ cm}$

Bài 7: Tam giác vuông có đường cao chia cạnh huyền thành hai đoạn 5 cm và 20 cm. Tính các cạnh của tam giác.

Lời giải

Cạnh huyền: $a = 5 + 20 = 25$ cm

Đường cao: $h = \sqrt{5 \times 20} = \sqrt{100} = 10$ cm

Cạnh góc vuông thứ nhất: $b = \sqrt{25 \times 5} = \sqrt{125} = 5\sqrt{5} \approx 11{,}18 \text{ cm}$

Cạnh góc vuông thứ hai: $c = \sqrt{25 \times 20} = \sqrt{500} = 10\sqrt{5} \approx 22{,}36 \text{ cm}$

Bài 8: Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Biết $BH = 4$ cm, $AH = 6$ cm. a) Tính $AB$, $CH$, $AC$, $BC$ b) Tính diện tích tam giác $ABC$ c) Tính chu vi tam giác $ABC$

Lời giải

a) Tính $AB$: $AB = \sqrt{AH^2 + BH^2} = \sqrt{6^2 + 4^2} = \sqrt{52} = 2\sqrt{13} \text{ cm}$

Tính $BC$: Từ $AB^2 = BC \cdot BH$: $BC = \frac{AB^2}{BH} = \frac{52}{4} = 13 \text{ cm}$

Tính $CH$: $CH = BC – BH = 13 – 4 = 9 \text{ cm}$

Tính $AC$: $AC = \sqrt{BC \cdot CH} \text{ hoặc } AC = \sqrt{AH^2 + CH^2}$ $AC = \sqrt{6^2 + 9^2} = \sqrt{36 + 81} = \sqrt{117} = 3\sqrt{13} \text{ cm}$

b) Diện tích: $S = \frac{1}{2} \cdot BC \cdot AH = \frac{1}{2} \times 13 \times 6 = 39 \text{ cm}^2$

Hoặc: $S = \frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \times 2\sqrt{13} \times 3\sqrt{13} = 39 \text{ cm}^2$

c) Chu vi: $P = AB + AC + BC = 2\sqrt{13} + 3\sqrt{13} + 13 = 5\sqrt{13} + 13 \approx 31{,}03 \text{ cm}$

Bài 9: Tam giác vuông có cạnh huyền $a = 10$ cm. Tìm các cạnh góc vuông để đường cao có độ dài lớn nhất.

Lời giải

Gọi hai cạnh góc vuông là $b$ và $c$.

Ta có: $b^2 + c^2 = 100$ (Pythagore)

Đường cao: $h = \frac{bc}{10}$

Để $h$ lớn nhất thì $bc$ lớn nhất.

Áp dụng bất đẳng thức Cauchy: $bc \leq \frac{b^2 + c^2}{2} = \frac{100}{2} = 50$

Dấu “=” xảy ra khi $b = c$.

Khi đó: $b = c = \sqrt{50} = 5\sqrt{2}$ cm

Đường cao lớn nhất: $h_{max} = \frac{50}{10} = 5$ cm

Vậy tam giác vuông cân có đường cao ứng với cạnh huyền lớn nhất.

Bài 10: Chứng minh rằng trong tam giác vuông, nếu đường cao chia cạnh huyền thành hai đoạn có tỉ lệ $1:4$ thì tỉ số hai cạnh góc vuông là $1:2$.

Lời giải

Gọi $b’ = k$, $c’ = 4k$ với $k > 0$.

Cạnh huyền: $a = 5k$

Hai cạnh góc vuông: $b = \sqrt{a \cdot b’} = \sqrt{5k \cdot k} = k\sqrt{5}$

$c = \sqrt{a \cdot c’} = \sqrt{5k \cdot 4k} = 2k\sqrt{5}$

Tỉ số: $\frac{b}{c} = \frac{k\sqrt{5}}{2k\sqrt{5}} = \frac{1}{2}$

Vậy tỉ số hai cạnh góc vuông là $1:2$ (đpcm).

---

Để giúp các bạn học sinh có thêm tài liệu ôn thi hiệu quả, mình xin chia sẻ thêm file PDF bài tập được phân dạng rõ ràng theo từng chủ đề, giúp việc học trở nên dễ dàng và hệ thống hơn.

Tải file pdf

---

9.2 Bài tập từ luyện

Bài 1. Bạn Mây đi xe đạp từ nhà đến trường bằng xe đạp điện theo tuyến đường thẳng thường ngày. Đi được 1,8km thì gặp một đoạn đường đang sửa chữa nên bạn Mây phải đi vòng qua trạm xăng nên tính đến khi đến trường đã đi thêm 8km. Tính khoảng cách từ nhà bạn Mây đến trường theo tuyến đường thẳng thường ngày.

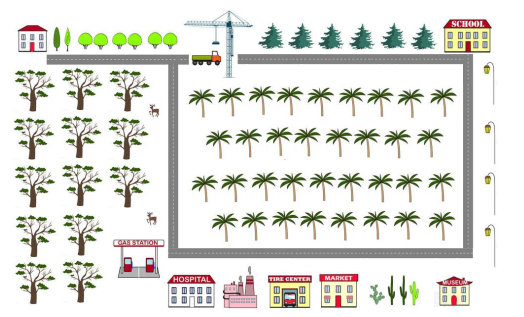
Bài 2. Hai bạn Vũ và Phúc đang ở hai đầu của một bể bơi, họ cùng bơi về phía bờ bên kia nơi có lá cờ. Bạn Vũ bơi với vận tốc 0,75m/s và bạn Phúc bơi với vận tốc 0,8m/s. Chiều rộng của bể là 12m và chiều dài là 25m. Tính thời gian mỗi bạn bơi tới lá cờ

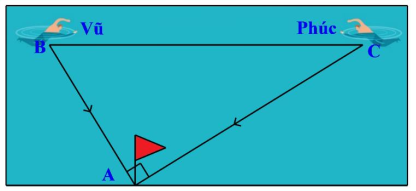
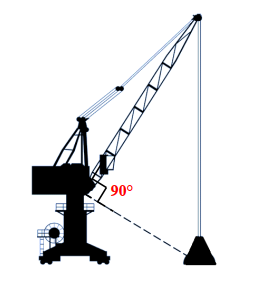
Bài 3. Một cần cẩu có cánh tay dài 8,5m đang nâng một vật lên cao như hình vẽ bên dưới. Biết vật cách thân cần cẩu là 5,5m. Hãy tính độ cao tối đa mà cần cẩu có thể nâng vật đó lên. Làm tròn kết quả đến hàng chục.

Bài 4. Một cây cau bị bão quật ngã vào bức tường và gãy ngang thân vô tình tạo thành một tam giác vuông. Hai người ở hai bên bức tường đo được khoảng cách từ gốc cau đến tường và khoảng cách từ ngọn cau đến tường lần lượt là 80cm và 180cm. Tính chiều cao của bức tường và chiều cao của cây cau (không tính phần tàu lá) khi chưa bị bão quật ngã.

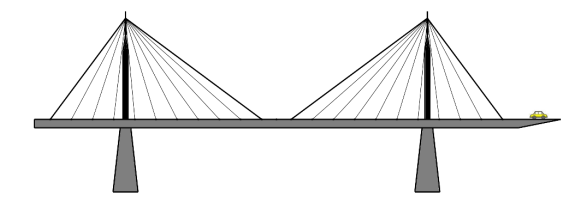
Bài 5. Cầu dây văng dạng rẻ quạt như hình vẽ bên dưới. Khoảng cách từ dây văng ngoài cùng đến trụ tháp lần lượt là 100m và 169m. Tính chiều cao của trụ tháp tính từ mặt nước biết cầu cách mặt nước 35m và hai dây văng ngoài cùng của một trụ tháp tạo thành một góc vuông.

Bài 6. Một người dùng cách ngắm thước eke để đo chiều cao của một cái cây với cách đo được mô phỏng trong hình dưới đây. Chiều cao tính từ chân đến mắt quan sát là 180cm và người này đứng thẳng cách gốc cây 240cm. Hãy tính chiều cao của cây

9.3. Bài tập trắc nghiệm

Câu 1: Tam giác vuông có hai cạnh góc vuông là $a$ và $2a$. Cạnh huyền bằng:

• A. $3a$
• B. $a\sqrt{3}$
• C. $a\sqrt{5}$
• D. $2a\sqrt{2}$

Đáp án: C

Giải thích: $\text{Cạnh huyền} = \sqrt{a^2 + (2a)^2} = \sqrt{5a^2} = a\sqrt{5}$

Câu 2: Tam giác vuông có cạnh huyền 13 cm, một cạnh góc vuông 5 cm. Đường cao ứng với cạnh huyền bằng:

• A. $\frac{60}{13}$ cm
• B. $6$ cm
• C. $\frac{65}{13}$ cm
• D. $12$ cm

Đáp án: A

Giải thích:

• Cạnh góc vuông còn lại: $c = 12$ cm
• Đường cao: $h = \frac{5 \times 12}{13} = \frac{60}{13}$ cm

Câu 3: Cho tam giác vuông có $\sin \alpha = 0{,}8$. Khi đó $\cos \alpha$ bằng:

• A. $0{,}2$
• B. $0{,}4$
• C. $0{,}6$
• D. $0{,}8$

Đáp án: C

Giải thích: $\cos^2 \alpha = 1 – \sin^2 \alpha = 1 – 0{,}64 = 0{,}36$, suy ra $\cos \alpha = 0{,}6$

10. Tóm tắt những điểm quan trọng

5 công thức vàng:

1. $a^2 = b^2 + c^2$
2. $h^2 = b’ \cdot c’$
3. $a \cdot h = b \cdot c$
4. $b^2 = a \cdot b’$, $c^2 = a \cdot c’$
5. ${\sin ^2}\alpha + {\cos ^2}\alpha = 1$

Sơ Đồ Tư Duy Tổng Hợp

                    HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
                                   |
                    ┌──────────────┴──────────────┐
                    |                             |
            CÁC YẾU TỐ                    CÁC HỆ THỨC
                    |                             |
        ┌───────────┼───────────┐        ┌────────┼────────┐
        |           |           |        |        |        |
    Cạnh huyền  Cạnh góc  Đường cao  Pythagore  Đường  Hình chiếu
        a        vuông b,c     h                 cao
                                                  |
                                        ┌─────────┴─────────┐
                                        |                   |
                                    h²=b'·c'            a·h=b·c
                                        |
                            ┌───────────┴───────────┐
                            |                       |
                        b²=a·b'                 c²=a·c'
                            |
                    TỈ SỐ LƯỢNG GIÁC
                            |
                ┌───────────┼───────────┐
                |           |           |
            sin=đối/huyền cos=kề/huyền tan=đối/kề
                            |
                    ┌───────┴───────┐
                    |               |
            sin²+cos²=1      tan·cot=1

Bảng Tra Cứu Nhanh

Công thức theo mục đích sử dụng

Cần tìm	Biết	Công thức
Cạnh huyền $a$	$b, c$	$a = \sqrt{b^2 + c^2}$
Cạnh góc vuông $b$	$a, c$	$b = \sqrt{a^2 – c^2}$
Cạnh góc vuông $b$	$a, b’$	$b = \sqrt{a \cdot b’}$
Đường cao $h$	$b’, c’$	$h = \sqrt{b’ \cdot c’}$
Đường cao $h$	$a, b, c$	$h = \frac{b \cdot c}{a}$
Hình chiếu $b’$	$a, b$	$b’ = \frac{b^2}{a}$
Góc $B$	$a, b$	$\sin B = \frac{b}{a}$
Cạnh $b$	$a, B$	$b = a \cdot \sin B$
Diện tích $S$	$b, c$	$S = \frac{1}{2}bc$
Diện tích $S$	$a, h$	$S = \frac{1}{2}ah$

Giá trị lượng giác đặc biệt (để tra nhanh)

Góc	sin	cos	tan	cot
$0°$	$0$	$1$	$0$	∞
$30°$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{3}}{3}$	$\sqrt{3}$
$45°$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{2}}{2}$	$1$	$1$
$60°$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\sqrt{3}$	$\frac{\sqrt{3}}{3}$
$90°$	$1$	$0$	∞	$0$

Bộ ba Pythagore thông dụng

Nhóm	Bộ ba cơ bản	Bội số ×2	Bội số ×3	Bội số ×5
I	(3, 4, 5)	(6, 8, 10)	(9, 12, 15)	(15, 20, 25)
II	(5, 12, 13)	(10, 24, 26)	(15, 36, 39)	(25, 60, 65)
III	(8, 15, 17)	(16, 30, 34)	(24, 45, 51)	(40, 75, 85)
IV	(7, 24, 25)	(14, 48, 50)	(21, 72, 75)	(35, 120, 125)
V	(20, 21, 29)	(40, 42, 58)	(60, 63, 87)	(100, 105, 145)

11. Mẹo Làm Bài Nhanh

Nhận biết nhanh tam giác vuông

• Nếu thấy bộ ba (3, 4, 5) hoặc bội số → Tam giác vuông
• Kiểm tra: $a^2 = b^2 + c^2$ (cạnh lớn nhất bình phương = tổng bình phương hai cạnh kia)

Tính nhanh đường cao

• Nếu biết hai cạnh góc vuông: $h = \frac{b \cdot c}{a}$ với $a = \sqrt{b^2 + c^2}$
• Bộ ba (3, 4, 5): $h = \frac{3 \times 4}{5} = 2{,}4$
• Bộ ba (5, 12, 13): $h = \frac{5 \times 12}{13} = \frac{60}{13}$

Sử dụng tam giác đặc biệt

Tam giác vuông cân (góc $45°-45°-90°$):

• Nếu cạnh góc vuông = $a$ → Cạnh huyền = $a\sqrt{2}$
• Nếu cạnh huyền = $a$ → Cạnh góc vuông = $\frac{a\sqrt{2}}{2}$

Tam giác nửa đều (góc $30°-60°-90°$):

• Cạnh đối $30°$ : Cạnh đối $60°$ : Cạnh huyền = $1 : \sqrt{3} : 2$
• Ví dụ: Nếu cạnh huyền = 10 → Cạnh đối $30°$ = 5, cạnh đối $60°$ = $5\sqrt{3}$

Kiểm tra nhanh kết quả

• Cạnh huyền > mọi cạnh góc vuông
• $b’ + c’ = a$ (hình chiếu)
• $h < b$ và $h < c$ (đường cao nhỏ hơn cạnh góc vuông)
• $0 < \sin, \cos < 1$
• $S = \frac{1}{2}bc = \frac{1}{2}ah$

Quy trình 5 bước giải bài tập

1. Đọc kỹ đề – Gạch chân thông tin quan trọng
2. Vẽ hình – Ghi rõ giả thiết, đánh dấu yếu tố cần tìm
3. Phân tích – Xác định công thức phù hợp
4. Tính toán – Thực hiện phép tính cẩn thận
5. Kiểm tra – Xem kết quả có hợp lý không

Câu hỏi thường gặp

Lời Kết

Hệ thức lượng trong tam giác vuông không chỉ là kiến thức để thi cử mà còn là công cụ hữu ích trong cuộc sống. Từ việc đo đạc đơn giản đến các ứng dụng công nghệ hiện đại, tam giác vuông luôn đóng vai trò quan trọng.